Estuary flow
The estuary scenario demonstrates in a basic manner how to calculate estuarine exchange flow by means of a water column model. Since the model has no resolution in horizontal direction, all horizontal gradients need to be prescribed. The barotropic pressure gradient is replaced by the vertically averaged time series of velocity to reproduce the tidal flow including the residual flow due to river run-off. This principle has been shown by Burchard (1999).
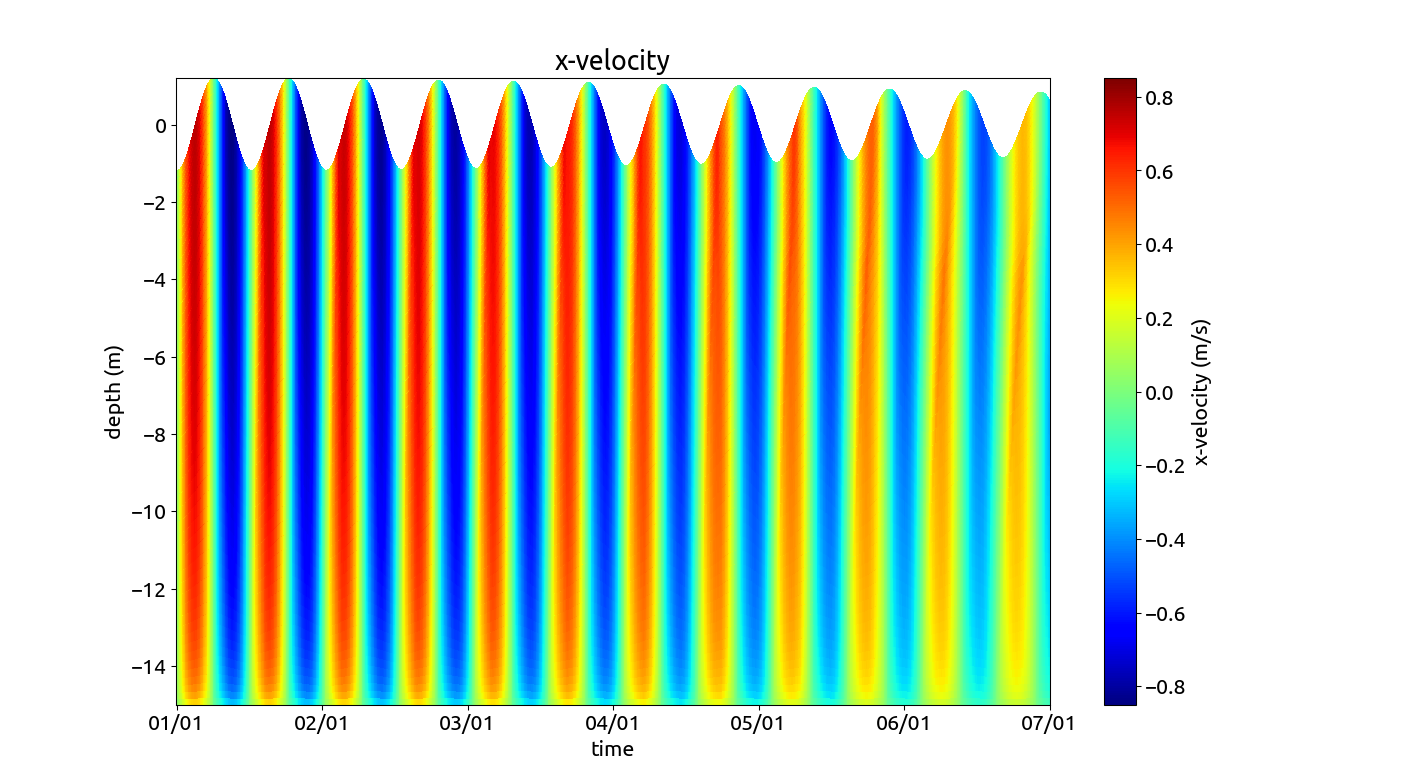
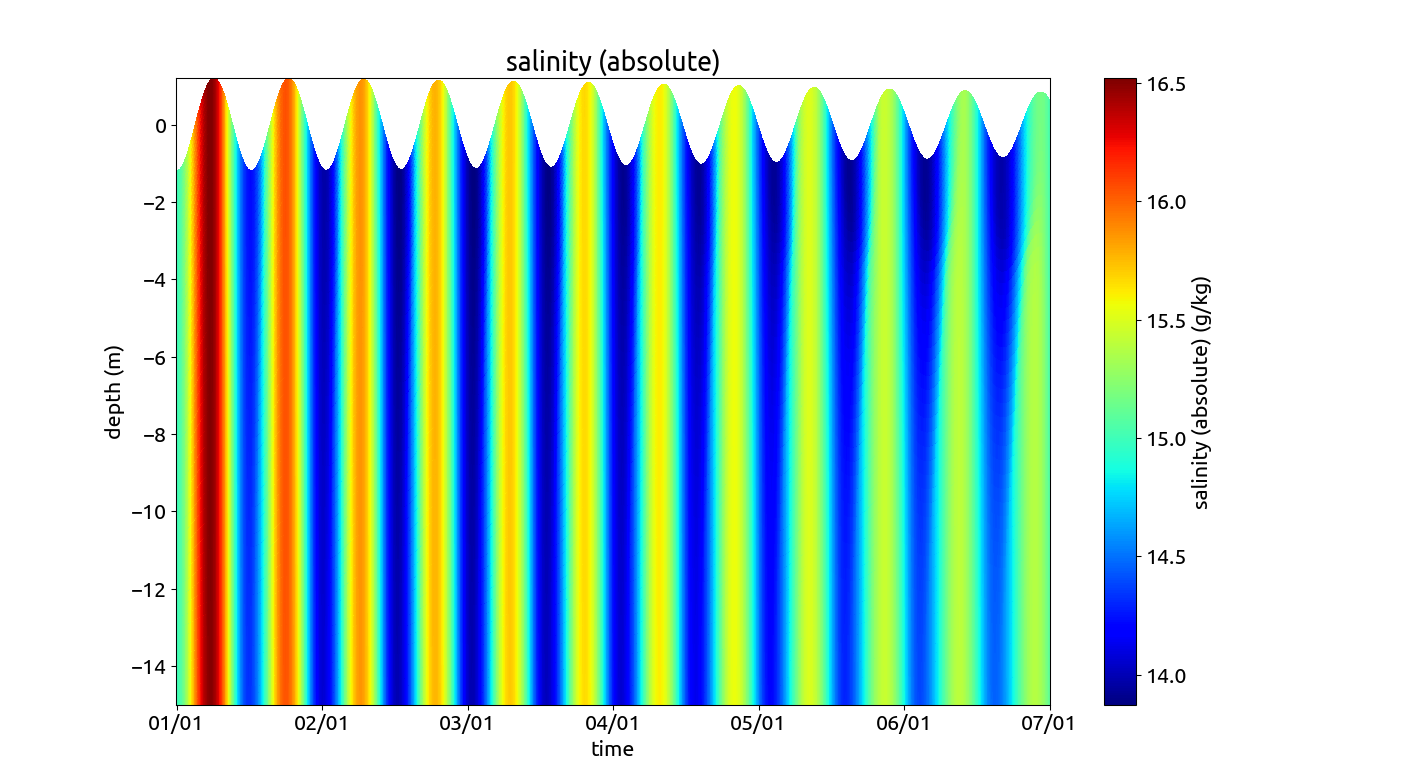
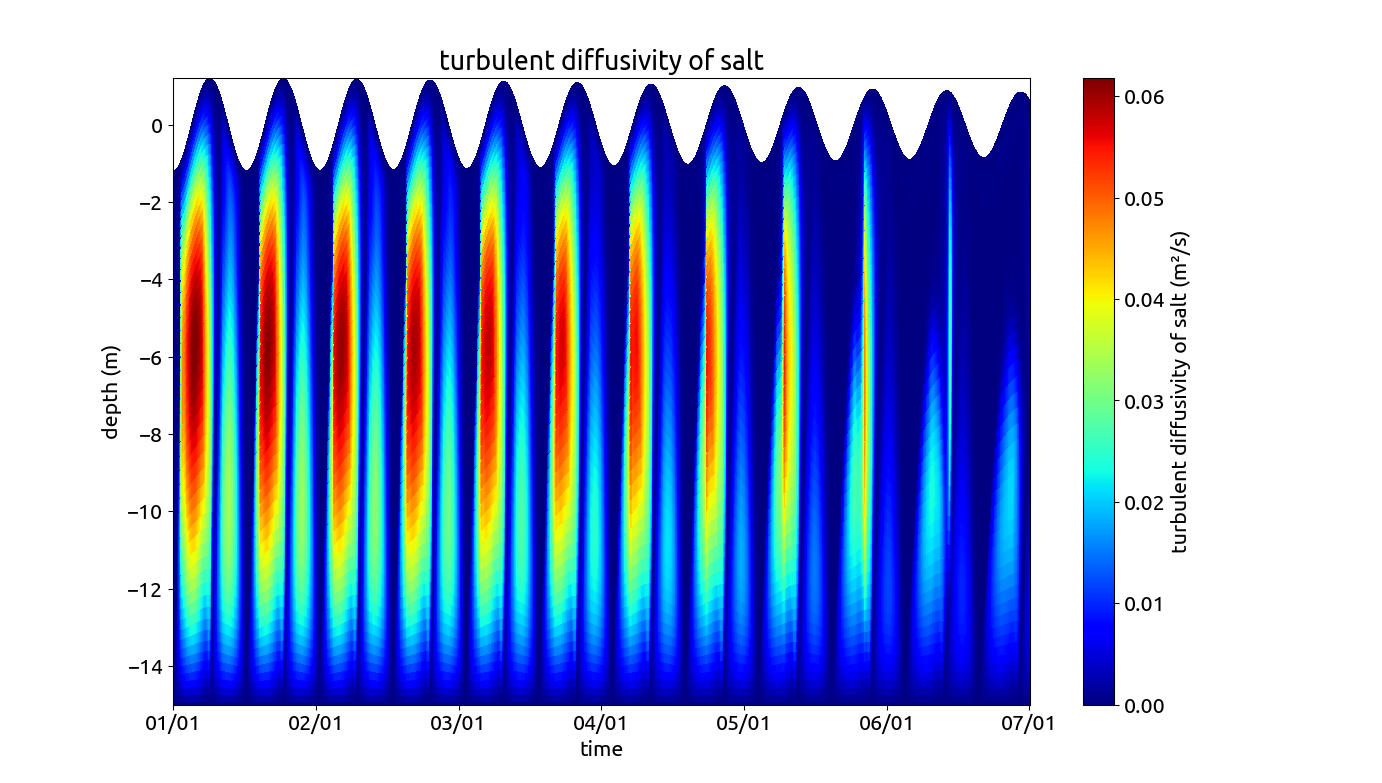
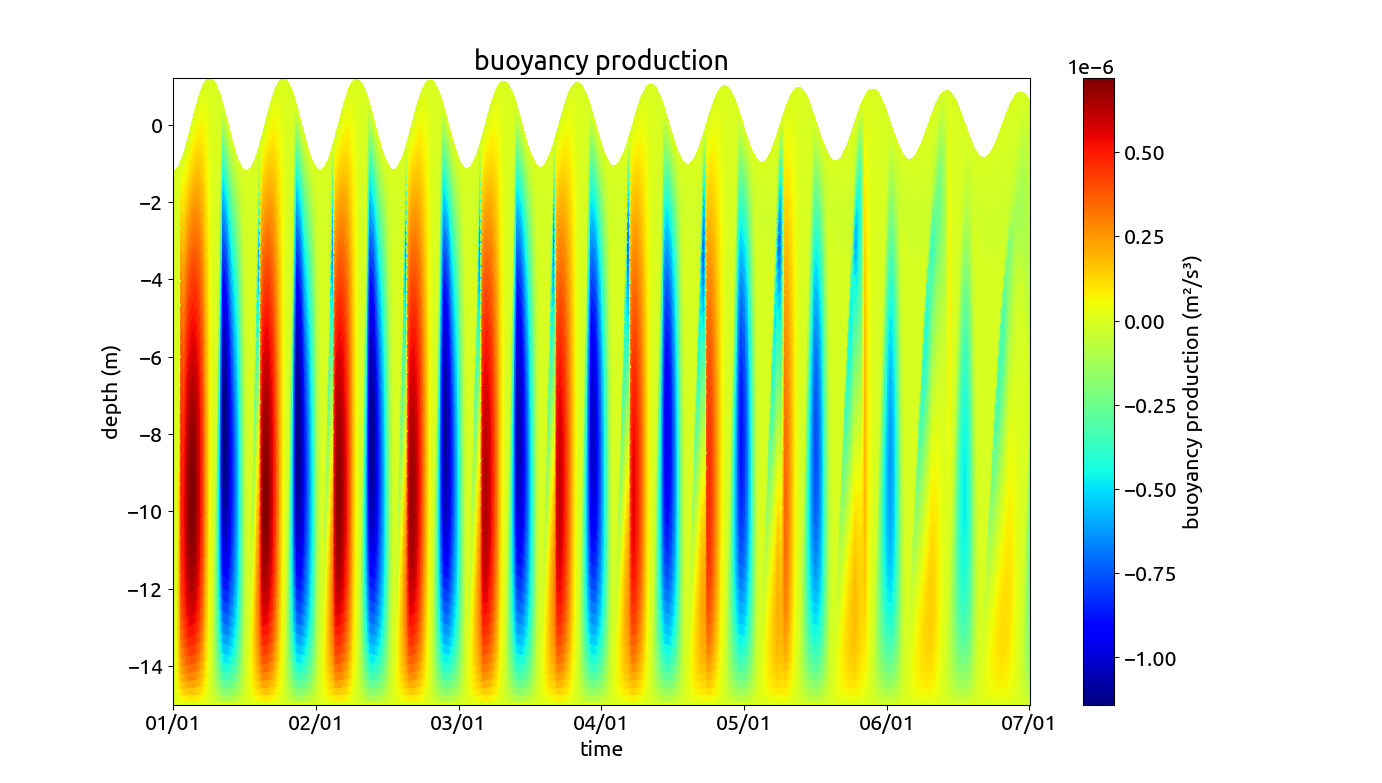
The internal pressure gradient is prescribed by means of a horizontal salinity gradient that is constant in time and space. From that, GOTM calculates the horizontal density gradient and the internal pressure gradient as well as the horizontal advection term for salinity. In addition to the pressure gradients, a free-surface tidal oscillation is added in a way that we have a standing tidal wave. Both, M~2~ and S~2~ tidal components are included, such that a spring-neap cycle is resulting (the simulation starts with a spring tide and moves half way toward a neap tide). In the figure below, the horizontal tidal velocity, the salinity, the eddy diffusivity and the buoyancy production are shown.
A typical SIPS (Strain-Induced Periodic Stratification) dynamics is developing, with destabilisation of the water column during flood (positive flow velocity, due to differential advection) and stabilisation during ebb flow (negative velocity). This type of estuary scenario has been applied in several publications such that in Burchard & Hetland (2010) and Burchard et al. (2023).
References:
Burchard, H., Recalculation of surface slopes as forcing for numerical water column models of tidal flow, Appl. Math. Modelling, 23, 737-755, 1999.
Burchard, H., and R.D. Hetland, Quantifying the contributions of tidal straining and gravitational circulation to residual circulation in periodically stratified tidal estuaries, J. Phys. Oceanogr., 40, 1243-1262, 2010.
Burchard, H., K. Bolding, X. Lange and A. Osadchiev, Decomposition of estuarine circulation and residual stratification under land-fast sea ice, J. Phys. Oceanogr., 53, 55-78, 2023.
Profiles of longitudinal velocity for the estuary scenario. Profiles of salinity for the estuary scenario. Profiles of eddy diffusivity for the estuary scenario. Profiles of buoyancy production for the estuary scenario.