
Numerical in-stabillities in the BBL
February 20, 2020
At the surface and the bottom, it is often desired to use a very high vertical resolution by setting the layer thicknesses to small values, i.e. to the order of 10 cm or less. This may become necessary when sediment concentrations need to be resolved near the bed or the wave-enhanced layer or primary production at low turbulence near the surface. In GOTM such high resolutions are achieved by setting ddu (for the surface) or ddl (for the bottom) to positive values, e.g. in the range of 1 … 3.
However, even though GOTM uses numerically implicit vertical diffusion for all state variables and the Patankar trick for the sink terms in the budgets of TKE and the turbulent length-scale related property (e.g., the TKE dissipation rate) to guarantee unconditional stability, some time step limitations exist.
When tides are present, it takes about 3 hours (e.g. from slack after ebb to full flood) to build up the maximum height of the bottom boundary layer (BBL). For a long time step, e.g. 1800s, and a thick bottom boundary layer, e.g. 30m, the thickness of the BBL might increase 5m or more during one time step. If the numerical layer thickness is small, e.g. 0.1m, the BBL has to pass of the order of 50 layers during one time step. Given the complex nonlinear dynamics of oscillating BBLs, this is certainly a great challenge for any turbulence closure model. It might be helpful to dig deeper into this problem and make a quantitative analysis to develop a time step criterium This would be an interesting task for the future. For the time being, it is sufficient to know that there is a time step criterium in the sense that dt/dz should be relatively small (but not necessarily smaller) compared to T/H with the tidal period T and the maximum mixed-layer depth H.
Here comes an illustration for the Flex scenario in GOTM. Compared to the standard settings, (ddl=ddu=0), ddl=3 and ddu=2 are chosen to give high resolution near the surface (about 0.2m) and near the bed (about 0.05m):
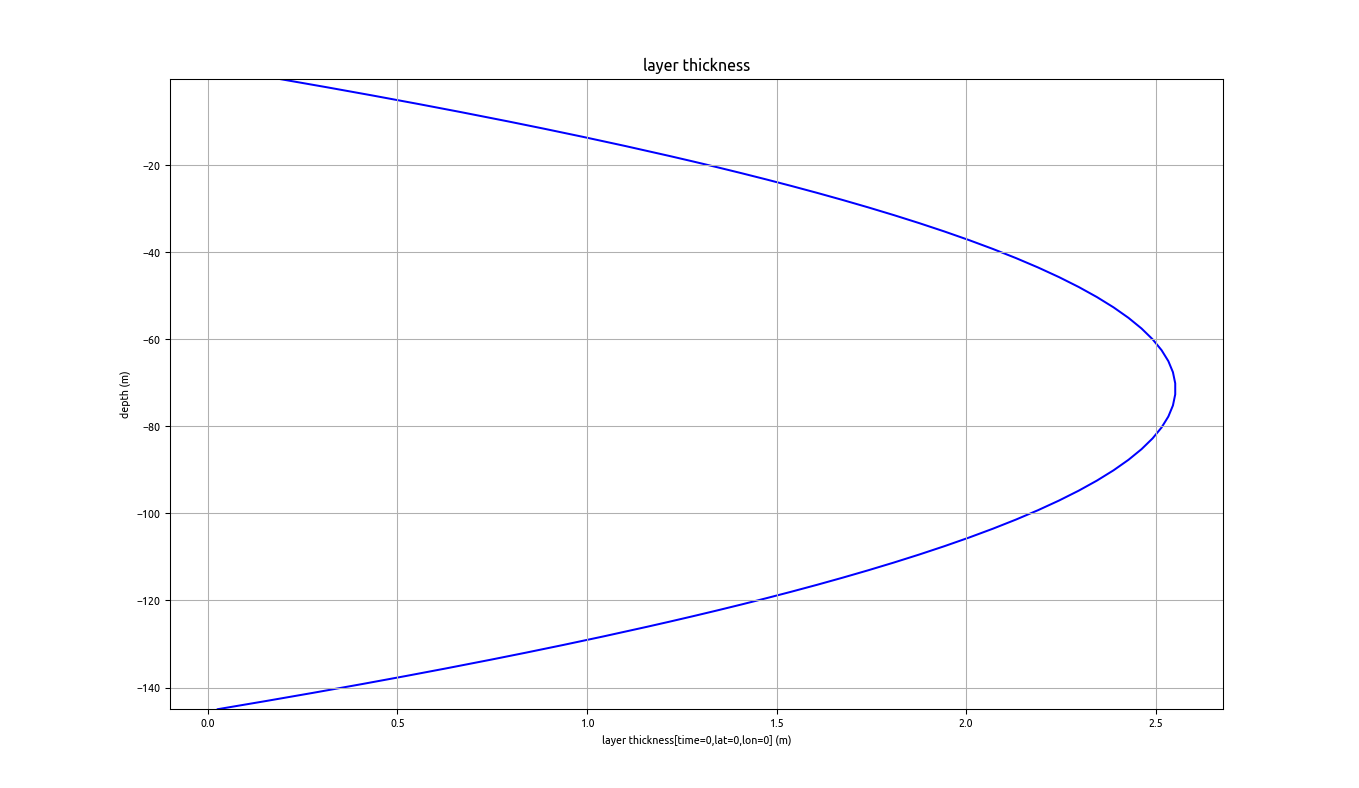
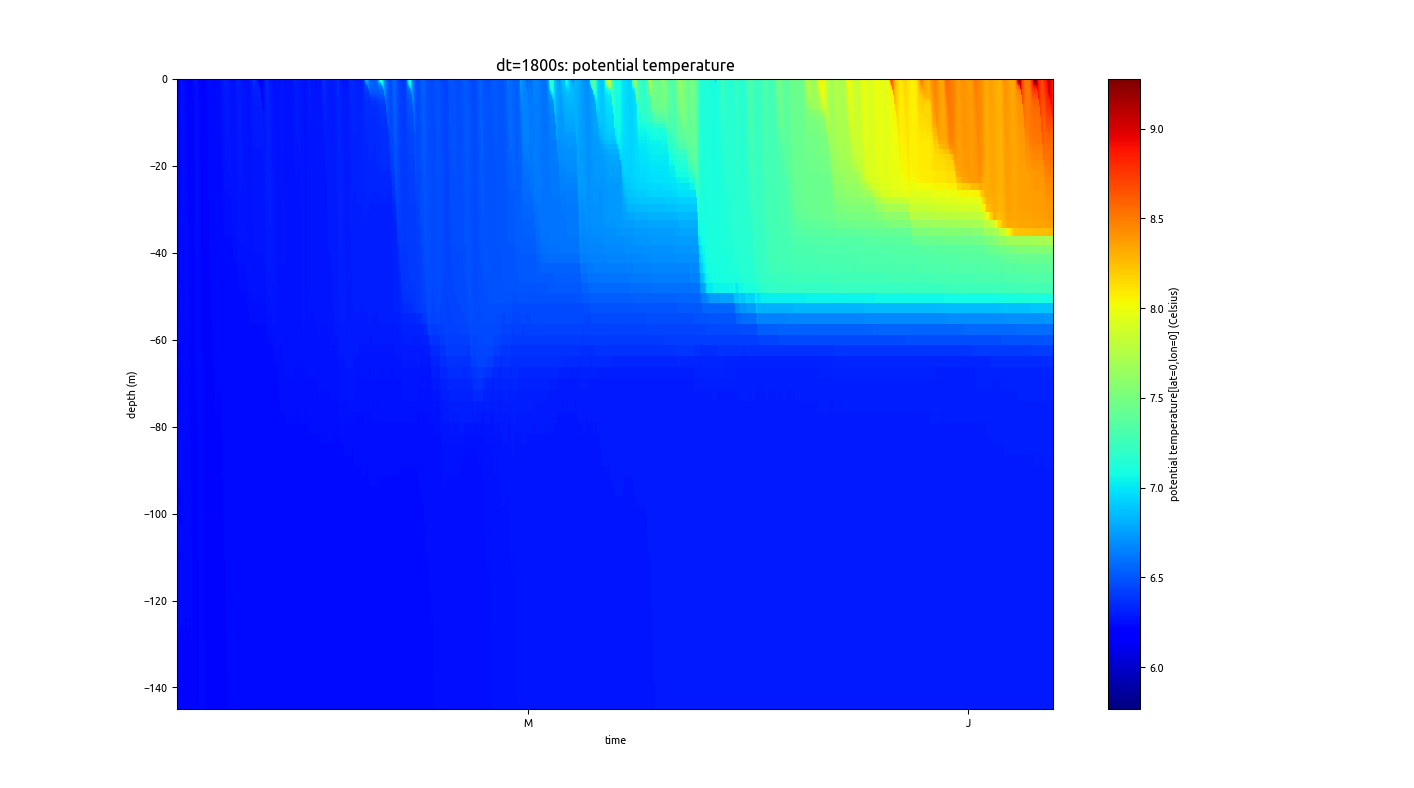
When we run the simulation with a time step of dt=1800s, the resulting temperature evolution looks stable and correct:
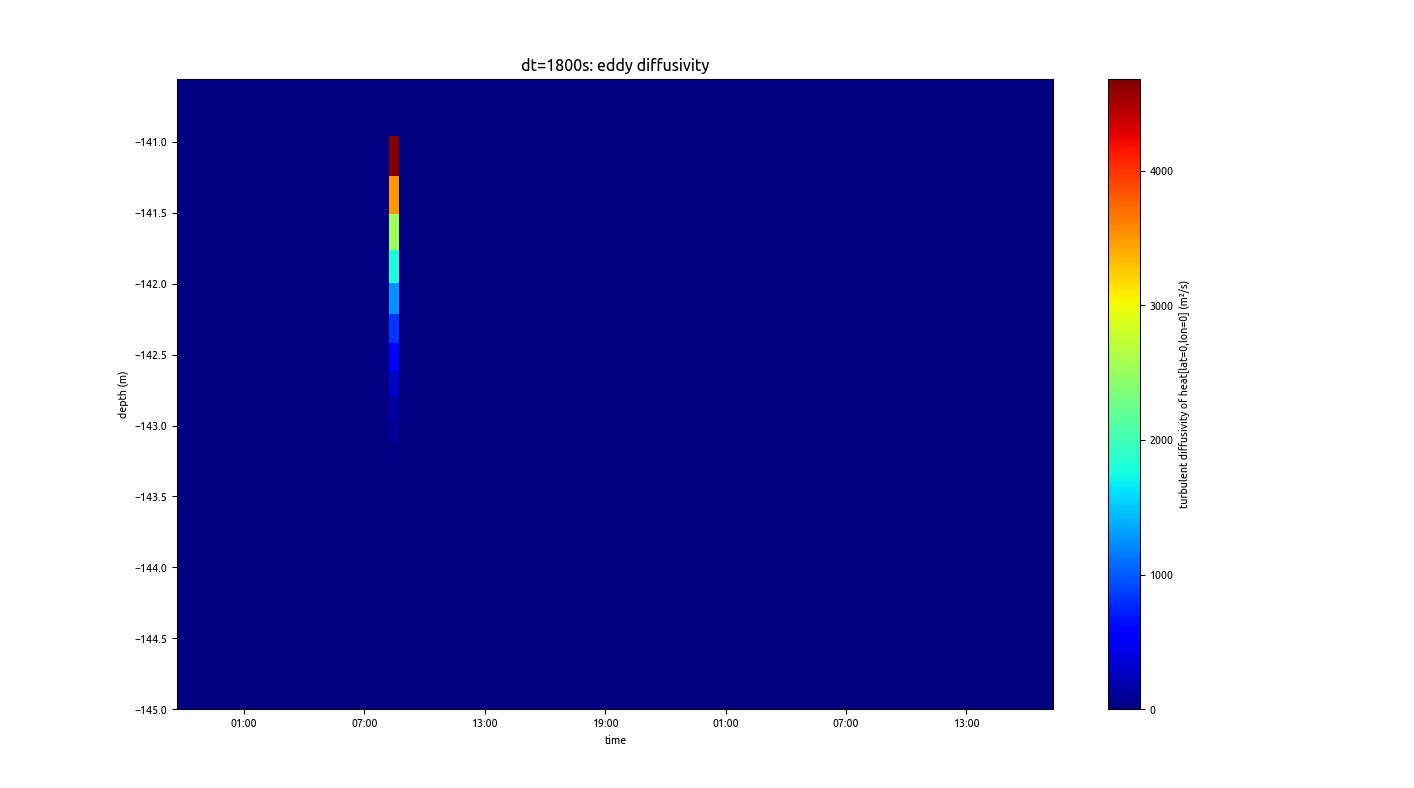
However, the overall evolution of the eddy diffusivity shows that there is a spike with values larger than 1000 m2/s:

A search for the location of these high values finds it in the BBL:
Only when reducing the time step (in this case dt=360s, the default value of the Flex scenario), the distribution of the eddy diffusivity looks reasonable:
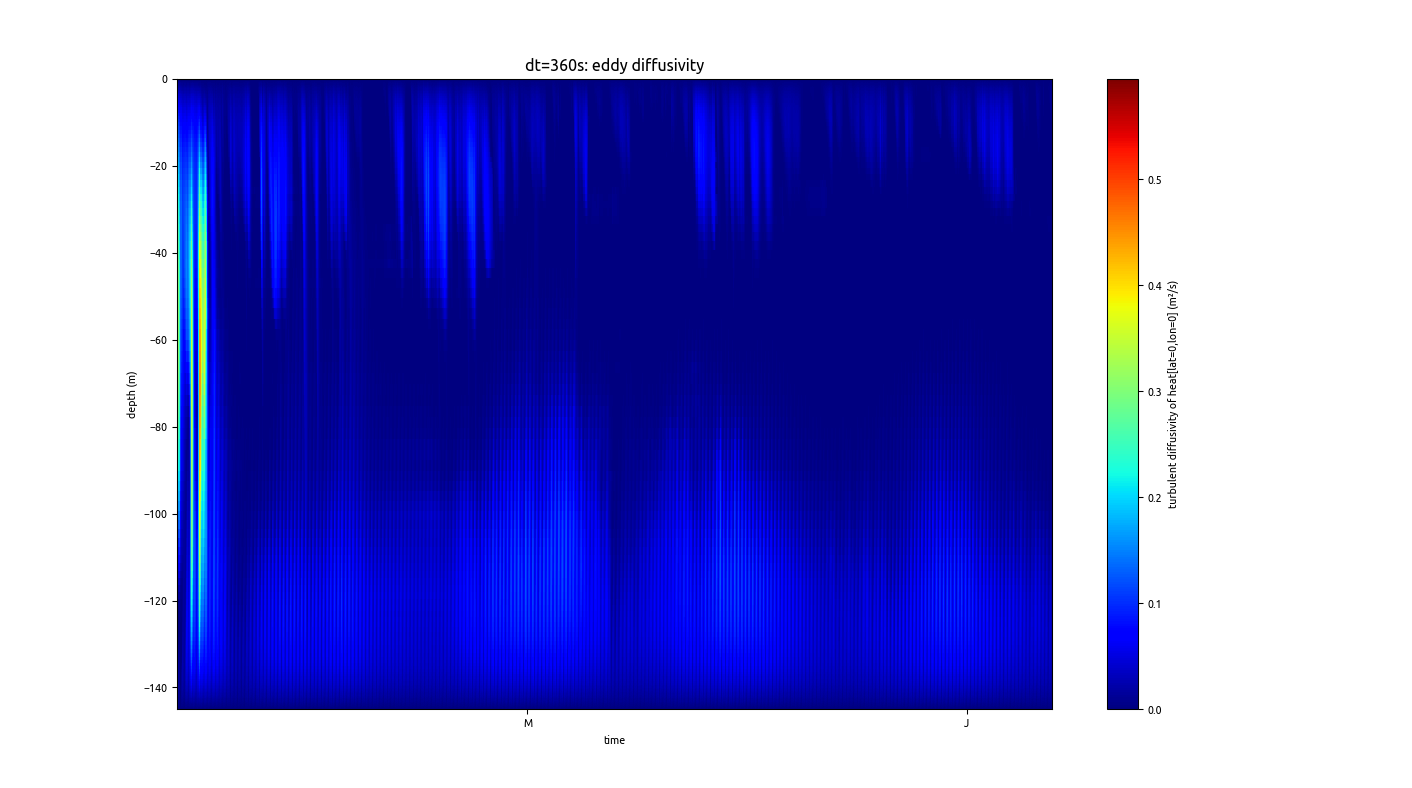
In this case we see that the BBL thickness grows to up to more than 50m, meaning that even for this short time step of 360s, given an average layer thickness in the BBL of dz=0.2 m over the lower 5m, and an increase of the BBL thickness of 50m during 3 hours, the BBL dynamics have to move across about 10 layers per time step. This seems to be still stable, but with a 5-fold time step of 1800s, 50 layers per time step are taken, leading to the spikes in eddy diffusivity.
It is remarkable, that this does not cause a blow-up of the simulation and that the temperature evolution still is accurate. The latter is the case, because temperature in the BBL is fully mixed and is therefore not affected by the super-high diffusivity. However, if e.g. sediment dynamics would have been included in the simulation, a vertical homogenisation of the sediment concentration would have resulted, destroying the sediment stratification.
In summary, for each GOTM simulation it is recommend to also check the sanity of the turbulence properties when analysing the results of a simulation.